
コンピュータで浮動小数点を扱う場合,さまざまな表現で記載することができる.この表現方法を統一するためにIEEE754という規格がある.
IEEE754
IEEE754には32ビット形式と64ビット形式がある.
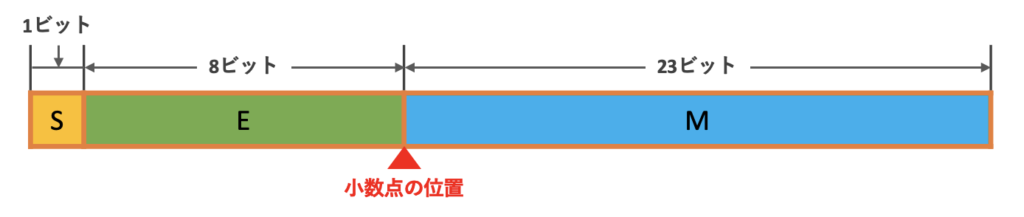
| 仮数部の符号 | S(0または1) |
| 指数部 | E |
| 仮数部 | M |
| 浮動小数点で表現される値 | \((-1)^S\times2^{E-127}\times(1+M)\) \((1+M)\)がある時は\(1.・・・・・\)の形式に正規化される |
10進数の少数からIEEE754形式の2進数への変換方法
例として\((3.125)_{10}\)をEEE754形式に変換する
1. 2進数に変換する
\(3.125=11.001\)
2. 符号をつけて浮動小数点の形式にする
\(+11.001\times2^0\)
3. 小数点と指数の位置を変更して正規化する
\(+1.1001\times2^1\)
4. 定められた形式に当てはめる
- \(S=0\) (正は0,負は1)
- \(E=((1+127)_{10})_{2}=((128)_{10})_{2}=1000 ~ 0000\) (指数+127の値の2進数)
- \(M=1001 ~ 0000 ~ 0000 ~ 0000 ~ 0000 ~ 000\) (仮数-1を左詰めで余ったビットには0を入れる)
\((3.125)_{10}\)をEEE754形式に変換すると下記になる
\(0 ~ 1000 ~ 0000~~1001 ~ 0000 ~ 0000 ~ 0000 ~ 0000 ~ 000\)




